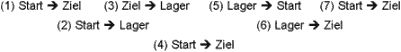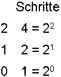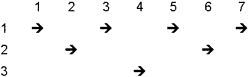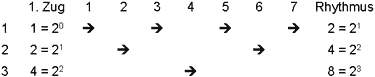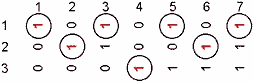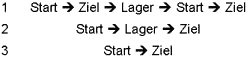Die Türme von Hanoi (The Towers of Hanoi)

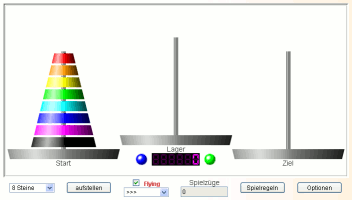
Dargestellt wird das mathematische Problem der Türme von Hanoi, hier mit bis zu 16 Steinen spielbar. Neben der klassisch rekursiven Lösung wurde für das Spiel eine iterative verwendet, die jederzeit eine Unterbrechung des Spiels gestattet.

Wird die Seite erneut geladen (Schaltfläche), kann die Höhe der Türme festgelegt, eine Statistik der Spielzüge angezeigt und Schaltflächen für eine automatische Lösung aktiviert werden.

Zum Spiel 'Die Türme von Hanoi' (Popup-Fenster)

Spielfeld (Ampel nur im Lösungsmodus)

Optional: Elemente des Lösungsmodus

Optional: Statistik der Spielzüge

Nebenbei wurde ein Kalender implementiert, für den u.a. der klassische Sortieralgorithmus Shell-Sort nach D.L. Shell und die Bestimmung von Ostern nach C.F. Gauss Verwendung fand.

Miniaturisiertes Hanoi-Spiel mit reduzierter Funktionalität und einem automatischen Start nach dem Laden des Spiels.

Zum Spiel 'Die Mini-Türme von Hanoi' (Popup-Fenster)

Theoretische Entwicklung sowohl der klassisch rekursiven als auch einer iterativen Lösung des Hanoi-Problems. Wie immer in leicht faßlicher Form.

Das Problem der Türme von Hanoi (Towers of Hanoi, ToH) wurde 1883 von dem französischen Mathematiker Edouard Lucas vorgeschlagen (Ottmann¹). Es beruhe auf einer alten Sage, wonach Mönche in einem Brahma-Tempel in der Nähe von Hanoi an einem solchen Puzzle mit 64 Steinen arbeiten (Müller²). Sowie dieses Puzzle gelöst sei, sei das Ende der Dinge gekommen.

• Es gibt drei Turmplätze als allein gültige Aufenthaltsorte für n Spielsteine unterschiedlicher Größe.
• Die Spielsteine sind zu Beginn von unten nach oben mit abnehmender Größe auf einem Turmplatz aufgeschichtet.
• Sie sollen in gleicher Anordnung auf einen anderen bestimmten (oder unbestimmten) Turmplatz gebracht werden.
• Zu jedem Zeitpunkt kann nur ein Stein, der oberste eines Turmes, bewegt werden.
• Kein Stein darf auf einem kleineren liegen.

Das Spiel soll auf dem PC spielbar sein. Die Lösung soll dargestellt werden.

Die sinnvolle Zerlegung eines Problems in kleinere und deren Lösung, so eine Strategie, löst durch Zusammensetzen auch das Gesamtproblem. Da führt René Descartes³ die Feder, dessen zweite Regel zu seiner "Methode des richtigen Vernunftgebrauchs und der wissenschaftlichen Forschung" ("Méthode pour bien conduire sa raison et chercher la verité dans les sciences") besagt, "jedes Problem ... in so viele Teile zu teilen, wie es angeht und wie es nötig ist, um es leichter zu lösen". Ottmann hebt dabei das Entwurfsprinzip "Teile und herrsche" (Divide and Conquer, D&C) hervor, wobei das Zusammenfügen (Merge) in der Bezeichnung nicht zum Ausdruck kommt, Müller die Alternativen Iteration vs. Rekursion und Solymosi/Grude⁴ das Prinzip der mathematischen Induktion, wonach mit einem trivialen Beweis für n = 1 oder n = 0 und einem zweiten Beweis für den Schluß von n auf n + 1 der Gesamtbeweis eines Satzes für jede natürliche Zahl erbracht ist.

Der triviale Algorithmus ist die Lösung eines Spiels mit einem Spielstein (n = 1): Man legt ihn in einem Zug vom Start-Turm auf den Ziel-Turm.

Umgangssprachlich formuliert könnte man codieren:

Funktion EinSteinBewegen(n Steine, Start, Ziel)
 
  Bewege Stein n vom Start zum Ziel.

Ganz so trivial ist dieser Schritt seiner Mehrdeutigkeit wegen allerdings nicht. Hat man mit diesem Stein nun alle vorhandenen oder den obersten oder den untersten auf den Ziel-Turm bewegt? Ist damit das Gesamtproblem gelöst oder handelt es sich um ein Elementarproblem? Hier fällt alles noch zusammen. Fest steht, daß es unter den gegebenen Bedingungen möglich ist, im allgemeinen einen Stein zu bewegen und im besonderen ins Ziel zu bewegen und damit die Aufgabe zu lösen.

Der Algorithmus für n + 1, also für zwei Spielsteine, liegt intuitiv auch sofort auf der Hand: In drei Spielzügen legt man den ersten Stein auf den Lagerplatz, den zweiten auf den Zielplatz und dann den ersten vom Lagerplatz auf den zweiten. Die beiden Steine gehen sozusagen getrennte Wege.

Somit gibt es auch ein allgemeines Verfahren, zwei Steine von einem Turm zu einem anderen zu bringen. Es setzt sich aus drei gleichförmigen Elementarbewegungen zusammen. Das Gesamtproblem wurde aufgeteilt (Divide) und jedes seiner Teile mit einem bekannten elementaren Algorithmus beherrscht (Conquer). Das Zusammenfügen (Merge) besteht in der richtigen Anordnung der Elementarbewegungen. Umgangssprachlich formuliert lautet die Codierung für n = 2:

Funktion ZweiSteineBewegen(n Steine, Start, Ziel, Lager)
 
  Bewege Stein n - 1 vom Start zum Lager.
 
  Bewege Stein n vom Start zum Ziel.
 
  Bewege Stein n - 1 vom Lager zum Ziel.
 


Die Mehrdeutigkeiten beim Versuch, diese drei Züge zu fassen, sind auch hier noch nicht beseitigt. Hat man mit dem ersten Spielzug den obersten Stein bewegt und die übrigen zurückgelassen oder alle, die auf dem untersten Spielstein lagen und also den untersten zurückgelassen? Noch sind Formulierungen wie "Stein 1" und "Stein n - 1", "Stein 2" und "Stein n" identisch. Vergegenwärtigt man sich noch einmal die Intuition, so ging sie vom oberen Stein hinunter zum unteren, um von dort her seine erste Bewegung bestimmen zu lassen. Der obere Stein, so die gedankliche Strategie, ging bei seiner Trennung vom unteren diesem aus dem Weg und machte zugleich das Lager zum Ziel seiner ersten elementaren Bewegung und zum Start für seine zweite.

Wäre das Steinebewegen eine umfangreiche Prozedur, könnte man wegen der Gleichartigkeit der Bewegung für beide Steine auf die erste Funktion mit wechselnden Wegen zurückgreifen:

Funktion ZweiSteineBewegen(n Steine, Start, Ziel, Lager)
 
  Rufe EinSteinBewegen(Stein n - 1, vom Start, zum Lager).
 
  Rufe EinSteinBewegen(Stein n, vom Start, zum Ziel).
 
  Rufe EinSteinBewegen(Stein n - 1, vom Lager, zum Ziel).

Der Bedeutungswechsel der Turmplätze für die Züge des oberen Steins ist eine von mehreren Ideen bei der Konstruktion des allgemeinen Lösungsalgorithmus. Was für die aufrufende Funktion das Lager ist, ist für die aufgerufene das Ziel oder der Start.

Eine Funktion nun, die wahlweise ein oder zwei Steine bewegt, kann also lauten

Funktion EinZweiSteineBewegen(n Steine, Start, Ziel, Lager)
 
Wenn n = 1, dann
 
  Bewege Stein n vom Start zum Ziel.
 
Sonst
 
  Bewege Stein n - 1 vom Start zum Lager.
 
  Bewege Stein n vom Start zum Ziel.
 
  Bewege Stein n - 1 vom Lager zum Ziel.

Sie wäre gleichbedeutend mit der Funktion

Funktion EinZweiSteineBewegen2(n Steine, Start, Ziel, Lager)
 
Wenn n > 1, dann
 
  Bewege Stein n - 1 vom Start zum Lager.
 
Bewege Stein n vom Start zum Ziel.
 
Wenn n > 1, dann
 
  Bewege Stein n - 1 vom Lager zum Ziel.

So weit, so gut. Der Schritt zur Verallgemeinerung ist damit noch nicht vollzogen, und der Beweis der Richtigkeit für jede andere Anzahl von Steinen ist im Sinne des mathematischen Ideals der vollständigen Induktion hier noch nicht erbracht, wenn die Funktionstüchtigkeit für zwei Steine erwiesen ist. Mit dem dritten Stein wird die Schwachstelle dieser Konstruktion deutlich, die es zu beseitigen gilt.

Ohne eine Idee wird man nicht weiterkommen. Auf der Suche danach könnte zum Beispiel die Erkenntnis stehen, daß der unterste Stein für alle anderen Steine wie ein leerer Turmplatz wirkt und kein Hindernis darstellt. Ebenso gibt es für den obersten Stein überhaupt kein Bewegungshindernis. Er könnte sich auf allen anderen Steinen niederlassen. Diese und andere Überlegungen sind zwar zutreffend, führen aber zunächst nicht weiter. Später, wenn die Lösung einmal gefunden ist, wird man feststellen, daß sich Steine mit gerader Nummer nur auf Steine mit ungerader niederlassen und umgekehrt. Aber was hilft das?

Die weiterführende Idee besteht darin, den untersten Stein getrennt von allen anderen zu behandeln. Zusätzliche Steine werden in der Formulierung "Stein n - 1" untergebracht, um sich anschließend diesen beiden Teilproblemen zu widmen:

Funktion VersuchZumSteineBewegen(n Steine, Start, Ziel, Lager)
 
Wenn n = 1, dann
 
  Bewege Stein n vom Start zum Ziel.
 
Sonst
 
  Bewege Stein(e) n - 1 vom Start zum Lager.
 
  Bewege Stein n vom Start zum Ziel.
 
  Bewege Stein(e) n - 1 vom Lager zum Ziel.

Als zentraler trivialer Spielzug wird die Bewegung des untersten Steines vom Startplatz zum Zielplatz aufgefaßt und zuvor, falls vorhanden, die Bewegung aller anderen vom Startplatz zum Lagerplatz und danach vom Lagerplatz zum Zielplatz. Die Trennung (Divide) bei zwei Steinen erfolgte gedanklich also zwischen dem unteren und dem darüberbefindlichen, nicht zwischen dem oberen und dem darunterbefindlichen, auch wenn es bei zwei Steinen praktisch auf dasselbe hinausläuft. Man muß deshalb noch einmal erwähnen, daß diese Sichtweise weder für n = 1, noch für n = 2 Steine notwendig ist. Die Spielbedingung, nur den obersten Stein eines Turmes bewegen zu können, würde sogar die Trennung zwischen dem obersten und allen darunterliegenden nahelegen und für bis zu zwei Steinen auch funktionieren. Nur kommt einem schon beim dritten Stein die Lösung merkwürdig kompliziert vor. Aber wer sagt denn, daß das Gesamtproblem überhaupt lösbar ist?

Die beiden entstandenen Teilprobleme, eine Anzahl Steine zu bewegen, kommen doch bekannt vor. Sie können je für sich betrachtet werden. Sie passen idealerweise in die Strategie, ein Problem so zu teilen, daß einerseits elementare Probleme entstehen, die man beherrscht, und andererseits Teilprobleme, die die gleiche Strukur wie das Gesamtproblem aufweisen. Die Idee dabei ist, daß eine Funktion dann so lange ihre Teilprobleme selbst löst (Rekursion), bis nur noch elementare Probleme übrigbleiben. Mit dieser Taktik kommt man auch einer Salami bei, von der man so lange eine Scheibe abschneidet, bis auch das letzte Stück nur noch eine Scheibe und damit gegessen ist.

Die Vergleichbarkeit der Problemstruktur muß genau geprüft werden. Sie wird hier dadurch gewährleistet, daß der unterste Stein die Bewegung aller übrigen nicht hemmt. Die Funktion würde sich also zweimal selbst aufrufen mit einer verminderten Anzahl und mit veränderten Wegen. Diese Aufrufe arbeiten unabhängig vom ursprünglichen Funktionsaufruf, wie eine andere Funktion es auch tun würde.

In der umgangssprachlichen Codierung hieße das:

Funktion SteineBewegen (n Steine, Start, Ziel, Lager)
 
// für Stein 1
 
Wenn n = 1, dann
 
  Bewege Stein n vom Start zum Ziel.
 
// für alle Steine außer Stein 1
 
Sonst
 
  Rufe Funktion SteineBewegen ((mit) n - 1 Steine, (vom) Start, (zum) Lager, (über) Ziel).
 
  Bewege Stein n vom Start zum Ziel.
 
  Rufe Funktion SteineBewegen ((mit) n - 1 Steine, (vom) Lager, (zum) Ziel, (über) Start).
 


Mit diesem klassischen Algorithmus ist das Gesamtproblem für jede Anzahl von Spielsteinen mit einem Schlag gelöst, denn alle Teilprobleme löst die Funktion, indem sie sich ggf. immer wieder selbst aufruft. Mit jedem neuen Aufruf wechselt die Bedeutung der einzelnen Plätze, ohne daß beim Zurückkehren an die aufrufende Stelle die dort gültigen Bedeutungen verloren gingen. Der oberste Stein wird als erster Stein (n = 1) oder als letzte Scheibe angesehen und mit einer elementaren Anweisung bewegt. Diese dient, wie bei jeder Rekursion aus naheliegenden Gründen notwendig, als ihre Abbruchbedingung.

Bevor beispielsweise der erste von fünf Steinen bewegt wird, ist die Funktion fünfmal aufgerufen worden, ohne daß die jeweiligen Prozeduren beendet wären: Das erste Mal von außen und viermal von sich selbst. Man überläßt es dem Verarbeitungsstapel des Betriebssystems, mit dieser vielfachen Rekursion fertigzuwerden und den für die Variablen notwendigen Speicherplatz zu organisieren.

Ganz Ausgebuffte verkürzen die bedingte Anweisung noch, so daß nun auch der erste Stein als ein unterster Stein aufgefaßt wird, über dem sich eine gewisse Anzahl von Steinen befindet. Kein Scherz. Sie werden ebenso wie alle tatsächlichen Steine eines Funktionsaufrufes für würdig befunden. Nur rufen in diesem sehr häufigen Fall die beiden zusätzlichen Rekursionen (mit n - 1, also mit 0) keine Wirkung hervor und beenden so auch die Rekursion. Die Verkürzung des Algorithmus geht zu Lasten des Verabeitungsstapels. Im Bild der Salami würde man nach der letzten Scheibe also noch einmal das Messer heben und alle Vorbereitungen treffen, um eine Scheibendicke über das Ende hinaus den nächsten Schnitt zu führen, ... und es dann aber unverrichteter Dinge wieder beiseite legen.

Funktion Steinbewegen (mit n Steinen, vom Start, zum Ziel, über Lager)
 
Wenn n > 0, dann
 
  Rufe Funktion Steinbewegen ((mit) n - 1 Steine, (vom) Start, (zum) Lager, (über) Ziel).
 
  Bewege Stein n vom Start zum Ziel.
 
  Rufe Funktion Steinbewegen ((mit) n - 1 Steine, (vom) Lager, (zum) Ziel, (über) Start).
 


Bei der Betrachtung eines Spiels mit drei Spielsteinen können einzelne Aspekte verdeutlicht und ein weiterer Lösungsalgorithmus angedeutet werden, der in einen geradezu geistlosen dritten mündet.

Der unterste Spielstein wird direkt ins Ziel bewegt (4), alle anderen darüber zunächst ins Lager, dann ins Ziel.

Diese beiden Teilprobleme werden jeweils für sich betrachtet und gelöst. Beim ersten Teilproblem wird das Lager zum Ziel, beim zweiten das Lager zum Start. Wieviele Steine auch immer vorhanden sind, alle über dem untersten gelangen zunächst ins Lager.

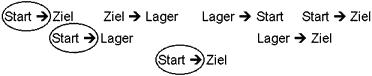
Alle Steine werden vom Startplatz aus bewegt, der oberste zuerst, der unterste zuletzt.

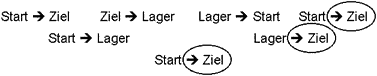
Alle Steine gelangen zum Zielplatz, der unterste zuerst, der oberste zuletzt.

Der unterste Stein bewegt sich in 1 Schritt, der nächste in 2, der nächste in 4. Der nächste wird 8 Schritte brauchen: Zweierpotenzen. Numeriert man die Steine von unten nach oben, angefangen bei i = 0, ergibt sich für jeden Stein i die Anzahl von 2ⁱ Zügen. Für die Summe der Spielzüge ergibt sich bei n Spielsteinen die Formel 2ⁿ - 1.

Bei der Frage, welcher Stein bei welchem Zug bewegt wird, ergeben sich zwei weitere Fragen: Wann wird ein Spielstein zum ersten mal bewegt? Und in welchem Rhythmus wird er sich fortan bewegen? Numeriert man diesmal die Steine von oben nach unten, beginnend mit 1, wird das Ergebnis deutlich, ebenfalls leicht ausdrückbar mit Zweierpotenzen.

Es geht aber noch einfacher. Drückt man die Spielzugnummer binär aus, so ist die Position des ersten auf 1 gesetzten Bits auch der Spielstein. Es ist die Position des Bits, das sich gerade von 0 auf 1 ändert.

Denkt man sich die drei Türme als im Kreis stehend, so stellt man beim Betrachten des Weges der Spielsteine fest, daß die Laufrichtung von Stein zu Stein wechselt. Läuft der unterste Stein, sagen wir, rechts herum, so der zweitunterste links herum und der darüber wieder rechts herum. Man könnte auch sagen, daß die einen Steine zum nächsten Turm weitergehen und die anderen zum übernächsten, was bei drei Türmen natürlich einem Schritt zurück gleichkommt.

Daß jeder Spielzugnummer genau ein Spielstein zugeordnet ist und für jeden Spielstein die Laufrichtung feststeht, wurde als alternativer Lösungsweg zur klassischen rekursiven Lösung im Demomodus implementiert.

Bestimmt man allerdings zu Beginn des Spiels die Laufrichtung des obersten Steins richtig, der ja jeden zweiten Zug für sich beansprucht (oder - wieder in Gegenrichtung - einen "Tabu-Turmplatz" für jeden Spielzug), so bleibt dem Spieler für den fälligen Zug zwischen den verbliebenen beiden Türmen wohl nichts anderes übrig als den kleineren Stein auf den größeren oder einen leeren Platz zu bewegen.

Wenn dann noch, wie z.T. vorgeschlagen wird, der Zielort beliebig einer der beiden leeren Türme ist, entfällt auch noch die einzig notwendige Anfangsüberlegung über die Richtung des ersten Zuges.

Die Mönche im legendären Brahma-Tempel bei Hanoi werden mit ihren 64 Spielsteinen im günstigsten Fall nach 18.446.744.073.709.551.615 Spielzügen ihr Spiel beenden. Ob Ihnen währenddessen diese Regel auffällt? Die Frage ist nur: was machen sie dann?

---

	© Georg Frevel 05.2002

¹ Thomas Ottmann (Hrsg.): Prinzipien des Algorithmenentwurfs. 1998.
² Oliver Müller: Grundlagen der Programmierung. 1998.
³ René Descartes: Discours de la méthode, 1637. Übersetzt von Lüder Gäbe. 1960.
⁴ Andreas Solymosi / Ulrich Grude: Grundkurs Algorithmen und Datenstrukturen, 2000.